



Next: The wave-function for high
Up: Periodic Wave-Function
Previous: Periodic Wave-Function
Contents
In order to obtain periodic orbitals, starting from non periodic ones it is sufficient to replace the Cartesian coordinates 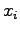 with a simple periodic function
with a simple periodic function 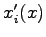 that take into account the appropriate periodicity of the box. In this thesis we used:
that take into account the appropriate periodicity of the box. In this thesis we used:
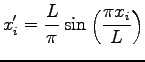 |
(4.3) |
and the new distance is defined as
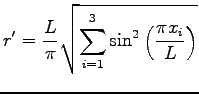 |
(4.4) |
In doing so, we have only to compute gradients and Laplacian with the chain rule:
where
This transformation has been applied to all orbitals appearing in the wave-function and also to the one-body term and the two-body Jastrow.
We remark here that also the normalization constant of a given orbital has to be changed in a periodic system. Namely its integral over the simulation cell has to be equal to one.
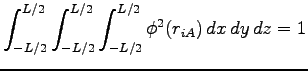 |
(4.5) |
For instance a normal Gaussian in three-dimension:
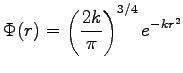 |
(4.6) |
becomes after the substitution 4.3:
![$\displaystyle \Phi'(r') = \left ( L e^{-\frac{k L^2}{\pi^2}} I_0 \left [ \frac{k L^2 }{\pi^2} \right ] \right )^{-3/2} e^{ -k r'^2}$](img414.png) |
(4.7) |
where 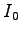 is the modified Bessel function of the first kind and
is the modified Bessel function of the first kind and  is the size of the simulation box and
is the size of the simulation box and  is the periodic distance 4.4.
is the periodic distance 4.4.




Next: The wave-function for high
Up: Periodic Wave-Function
Previous: Periodic Wave-Function
Contents
Claudio Attaccalite
2005-11-07
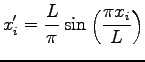
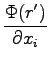
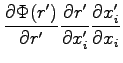
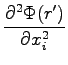
![$\displaystyle \frac{\partial^2 \Phi(r')}{\partial r'^2} \left ( \frac{\partial ...
... )^2 + \frac{\partial r'}{x_i'} \frac{ \partial^2 x_i'}{\partial x_i^2}\right ]$](img407.png)
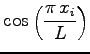
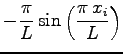
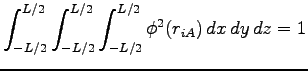
![$\displaystyle \Phi'(r') = \left ( L e^{-\frac{k L^2}{\pi^2}} I_0 \left [ \frac{k L^2 }{\pi^2} \right ] \right )^{-3/2} e^{ -k r'^2}$](img414.png)