



Next: How to evaluate pressure
Up: Coulomb Interactions in periodic
Previous: Ewald Sums
Contents
The method present in section 1.1.1 can be easily generalized to periodic systems. It is sufficient use an auxiliary periodic function
 with the same behavior of 1.12 close to nuclei. We have used the following form:
with the same behavior of 1.12 close to nuclei. We have used the following form:
where 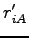 is the periodic distance between the nucleus
is the periodic distance between the nucleus  and the electron
and the electron  :
:
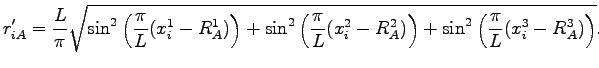 |
(4.18) |
Notice that
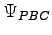 is a periodic function because we are using a periodic trial wave-function
is a periodic function because we are using a periodic trial wave-function  (see section 4.1.2).
This auxiliary function
(see section 4.1.2).
This auxiliary function
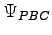 removes the divergence in the bare force and it is consistent with the periodicity of the system. At variance of the case without periodic boundary conditions
removes the divergence in the bare force and it is consistent with the periodicity of the system. At variance of the case without periodic boundary conditions
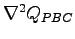 does not cancel exactly the term coming from the derivative of the ion-electron potential. Therefore we have to included both the Laplacian of the
does not cancel exactly the term coming from the derivative of the ion-electron potential. Therefore we have to included both the Laplacian of the 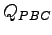 and the derivatives of the ion-electron potential in the calculation of the forces.
More precisely the expression we used for the force is:
and the derivatives of the ion-electron potential in the calculation of the forces.
More precisely the expression we used for the force is:
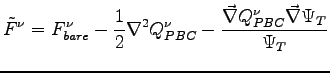 |
(4.19) |
where:




Next: How to evaluate pressure
Up: Coulomb Interactions in periodic
Previous: Ewald Sums
Contents
Claudio Attaccalite
2005-11-07
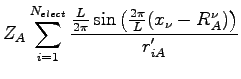
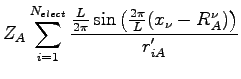
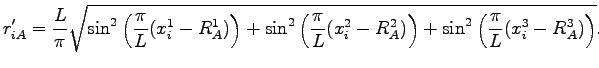
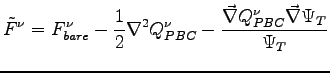
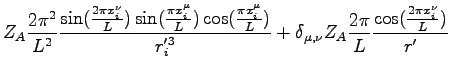
![$\displaystyle Z_A \sum_{\mu =1,3} -\frac{\pi^2}{L^2} \frac{\sin(\frac{2 \pi x^\...
...t ) \cos \left (\frac{\pi x_i^\mu}{L} \right ) \right]^2 \frac{1}{r'^2} \right.$](img482.png)
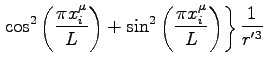
![$\displaystyle 2 Z_A \frac{\pi^2}{L^2} \left [-\sin \left (\frac{2 \pi x_i^\nu}{...
... \cos \left (\frac{2 \pi x_i^\nu}{L} \right) \frac{1}{r'^2}\right] \frac{1}{r'}$](img485.png)