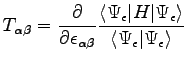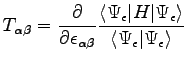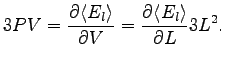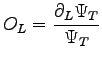Next: Empirical laws of melting
Up: Quantum Monte Carlo on
Previous: Forces with finite variance
Contents
How to evaluate pressure
Following the seminal paper of O.H. Nielsen an R.M. Martin Ref. (81), the pressure can be expressed as the negative trace of the stress tensor
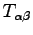 :
:
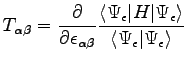 |
(4.20) |
where the
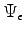 is the wave-function "stretched" by the transformation on each particle
is the wave-function "stretched" by the transformation on each particle
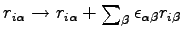 where
where
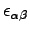 is a symmetric strain tensor. The pressure is then defined through the negative trace of the stress tensor:
is a symmetric strain tensor. The pressure is then defined through the negative trace of the stress tensor:
![$\displaystyle 3PV=-Tr [ T_{\alpha \beta} ]$](img491.png) |
(4.21) |
For an isotropic system, as the one we studied, the pressure can be easily written as:
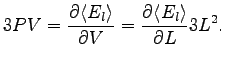 |
(4.22) |
where 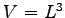 and
and  is the edge of our cubic box. To evaluate this derivative it is convenient to write the energy using rescaled distances that are invariant for stretching of the simulation box, namely
is the edge of our cubic box. To evaluate this derivative it is convenient to write the energy using rescaled distances that are invariant for stretching of the simulation box, namely 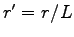 . After this transformation the expectation value of the energy can be written as:
. After this transformation the expectation value of the energy can be written as:
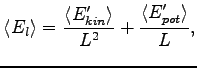 |
(4.23) |
where 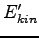 and
and 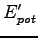 are the kinetic and the potential energy in the new coordinates. Thus the pressure will be:
are the kinetic and the potential energy in the new coordinates. Thus the pressure will be:
![$\displaystyle P = \frac{1}{3 V} \left [ 2 \frac{\langle E'_{kin} \rangle}{L^2} ...
...\left [ \langle O_L H \rangle - \langle O_L \rangle \langle H \rangle \right ],$](img498.png) |
(4.24) |
where 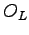 is the logarithmic derivative of the wave-function respect to the simulation box size
is the logarithmic derivative of the wave-function respect to the simulation box size  :
:
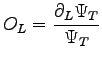 |
(4.25) |
Notice that the box size  appears in the one-body terms and in the two-body terms due to the cusp condistions, see Appendix C.
The first part of the expression 4.24 is the usual Virial Theorem and the second one is given by the contribution due to the Pulay stress tensor. In fact although we used rescaled coordinates, it is not possible to cancel the dependencies of the wave-function from the simulation box size. This is due to the nuclear and electronic cusp conditions that depend explicitly on
appears in the one-body terms and in the two-body terms due to the cusp condistions, see Appendix C.
The first part of the expression 4.24 is the usual Virial Theorem and the second one is given by the contribution due to the Pulay stress tensor. In fact although we used rescaled coordinates, it is not possible to cancel the dependencies of the wave-function from the simulation box size. This is due to the nuclear and electronic cusp conditions that depend explicitly on  (see Appendix C).
(see Appendix C).
In the expression 4.24 only the electronic kinetic energy is considered. When we perform a dynamic on the ionic part, we have to add the pressure due to the momentum flux carried by the ions. This part can be easily calculate with the standard kinetic theory (see Appendix B of Ref. (82)) of gas, and it reads:
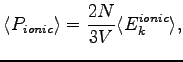 |
(4.26) |
the total pressure will be the sum of the ionic 4.26 and electronic part 4.24.




Next: Empirical laws of melting
Up: Quantum Monte Carlo on
Previous: Forces with finite variance
Contents
Claudio Attaccalite
2005-11-07