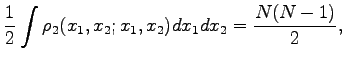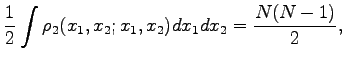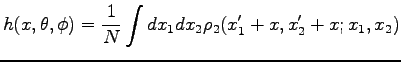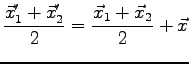Next: Conclusions
Up: Preliminary results on high
Previous: Pair Correlation Functions
Contents
The Resonant Valence Bond state has been shown to describe accurately frustrated spin systems. It appears that in many systems superconductivity is realized when the system in the normal state is quite close to metal-insulator transition even in presence of strong disorder, see Ref. (100). The large mass difference between ions and electrons leads, in a good approximation, to two distinct dynamics. This allows us to consider always the electrons in the ground state of a disordered ionic system
at finite temperature, and from this point of view it is "similar" to an average on disorder. Following this hypotheses we tried to study the possibility of stable superconducting phases driven by correlation close to the metal-insulator transition and solid-liquid transition. Moreover as in high-Tc superconductor, we expect that due to the small size of the Cooper pair a superconductive state can be more stable close to a disordered phase (101).
In order to detect superconductivity we have calculated the condensation energy on different configurations in the liquid phase, with VMC and DMC. The condensation energy, in a variational scheme, is defined as the energy difference obtained between the best Slater determinant, the normal state, and the AGP. In order to estimate the condensation energy we have reduced the rank of the pairing matrix to  . In such limit the pairing determinant is equivalent to a Slater one, as shown in (2). We optimized the Slater wave-function on given configurations and we found a non-zero condensation energy (see figure 6.5), namely a gain in energy given by allowing pairing within a variational ansatz.
At present we do not even know whether this gain in energy is macroscopic or is just a finite size effect even a the VMC level. The corresponding energy gain, obtained in this way, certainly overestimate a possible true condensation energy due to a real superconducting ground state for high pressure hydrogen. In fact the variational approach is certainly biased towards superconducting phases even though recently in the 2D Hubbard model there are other evidences of superconducting phase from non variational approaches (102).
. In such limit the pairing determinant is equivalent to a Slater one, as shown in (2). We optimized the Slater wave-function on given configurations and we found a non-zero condensation energy (see figure 6.5), namely a gain in energy given by allowing pairing within a variational ansatz.
At present we do not even know whether this gain in energy is macroscopic or is just a finite size effect even a the VMC level. The corresponding energy gain, obtained in this way, certainly overestimate a possible true condensation energy due to a real superconducting ground state for high pressure hydrogen. In fact the variational approach is certainly biased towards superconducting phases even though recently in the 2D Hubbard model there are other evidences of superconducting phase from non variational approaches (102).
As shown in the famous paper of Yang (103) a peculiar property of superconductors is the Off-Diagonal Long-Range Order (ODLRO) exhibited by the reduced density matrices in the coordinate space representation (103).
For Fermions ODLRO corresponds to the appearance of an eigenvalue which scales with the number of particles in the two-body density matrix (103):
where  is the number of particles.
In a translational invariant system, ODLRO implies for the two-body density matrix the following asymptotic behavior:
is the number of particles.
In a translational invariant system, ODLRO implies for the two-body density matrix the following asymptotic behavior:
where 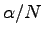 is the pair condensate fraction and
is the pair condensate fraction and  is the size of the pair defined by the pairing function
is the size of the pair defined by the pairing function  . The function
. The function  is zero for large separation
is zero for large separation
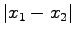 and is
and is
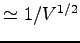 for microscopic separation for
for microscopic separation for 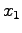 and
and 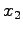 .
In order to
estimate the condensate fraction, following De Palo et al. (104), we resort
the two-body density matrix to the projected density matrix:
.
In order to
estimate the condensate fraction, following De Palo et al. (104), we resort
the two-body density matrix to the projected density matrix:
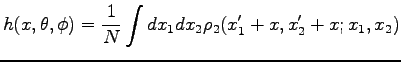 |
(6.6) |
which tends to  in the large x limit. The presence of non positive eigenvalues in the
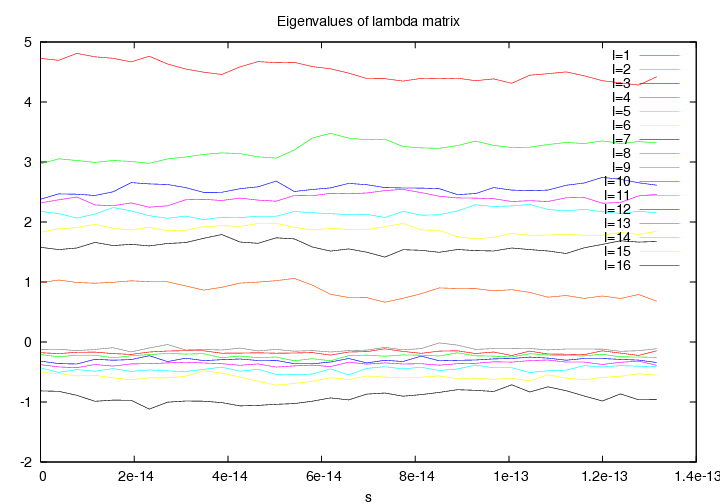
in the large x limit. The presence of non positive eigenvalues in the  matrix, see figure 6.6, led us to investigate the presence of non s-wave superconductivity. Therefore we also evaluated
matrix, see figure 6.6, led us to investigate the presence of non s-wave superconductivity. Therefore we also evaluated
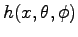 as a function of rotations angle
as a function of rotations angle
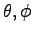 of the electron pair in order to investigate the possibility of different symmetries.
of the electron pair in order to investigate the possibility of different symmetries.
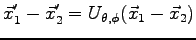 and and 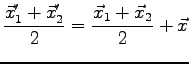 |
(6.7) |
A simple estimator of
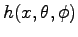 is given by
is given by
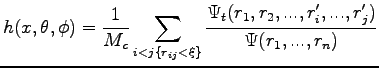 |
(6.8) |
where 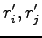 is an electron pair translated of
is an electron pair translated of  and rotated of
and rotated of
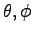 , and
, and 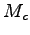 the number of pairs translated. A cutoff
the number of pairs translated. A cutoff  is introduced to speed up the calculation excluding contributions coming by pairs of far electrons that do not contribute to the ODLRO because the pairing is short range. We have verified that the cutoff used does not effect the final result.
In practice, for each pair we generate a few translations
is introduced to speed up the calculation excluding contributions coming by pairs of far electrons that do not contribute to the ODLRO because the pairing is short range. We have verified that the cutoff used does not effect the final result.
In practice, for each pair we generate a few translations  uniformly distributed in
the simulation box and, for better statistics, we also average over all pairs with the condition
uniformly distributed in
the simulation box and, for better statistics, we also average over all pairs with the condition
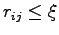 .
.
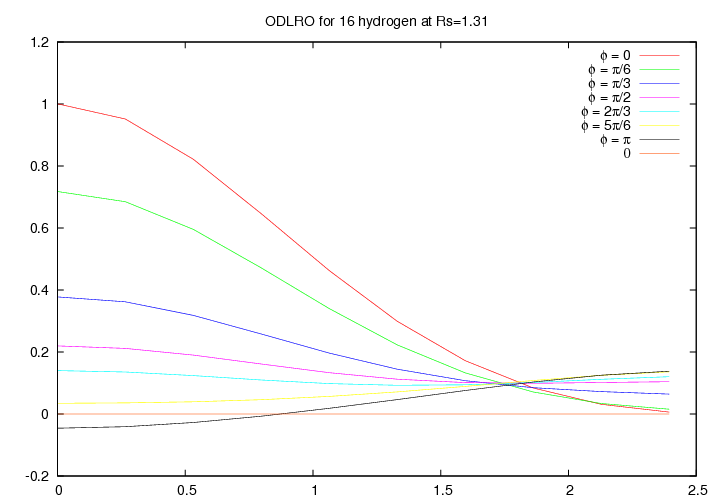
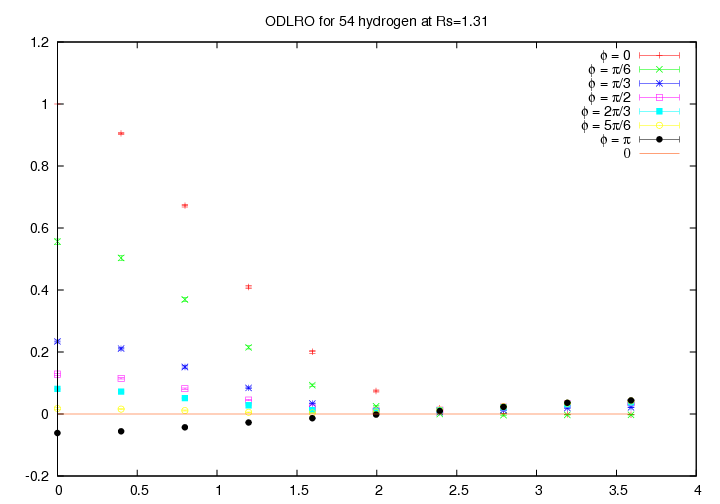
We argue the possibility of a non s-wave symmetry in the ODLRO, see figure 6.7 and 6.8. Unfortunately the size of the studied system is too small to give a conclusive answer.
Figure 6.5:
Variational and Diffusion Condensation Energy per atom
|
|
Figure 6.6:
Eigenvalues of the  matrix for 16 hydrogen atoms at Rs=1.31 and 100K as function of the simulation time
matrix for 16 hydrogen atoms at Rs=1.31 and 100K as function of the simulation time
|
|
Figure 6.7:
Off-Diagonal Long Range Order for 16 hydrogen atoms at Rs=1.31 and 100K, in a box of size  , for
, for  as function of the distance
as function of the distance 
|
|
Figure 6.8:
Off-Diagonal Long Range Order for 54 hydrogen atoms at Rs=1.31 at 100K in a box of size  , for
, for  as function of the distance
as function of the distance 
|
|




Next: Conclusions
Up: Preliminary results on high
Previous: Pair Correlation Functions
Contents
Claudio Attaccalite
2005-11-07