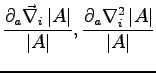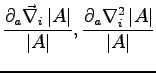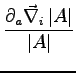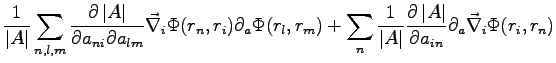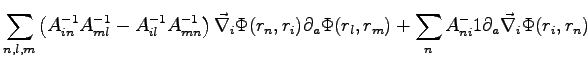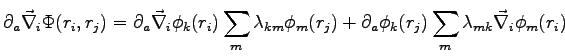Derivatives of the Local Energy

To evaluate the derivatives of the local energy we need to calculate the following terms:

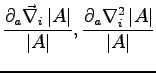$$\frac{\partial_a \vec{\nabla}_i \left\vert A \right\vert}{\left\v... ...\frac{\partial_a \nabla^2_i \left\vert A \right\vert}{\left\vert A \right\vert}$$ (B.23)

we obtain:

$$\frac{\partial_a \vec{\nabla}_i \left\vert A \right\vert}{\left\vert A \right\vert} = \frac{1}{\left\vert A \right\vert} \sum_{n,l,m} \frac{\partial \l... ...\vert A \right\vert}{\partial{a_{in}}} \partial_a \vec{\nabla}_i \Phi (r_i,r_n)$$

$$= \sum_{n,l,m}\left( A^{-1}_{in}A_{ml}^{-1} - A^{-1}_{il}A^{-1}_{mn... ...al_a \Phi(r_l,r_m) + \sum _n A_{ni}^-1 \partial_a \vec{\nabla}_i \Phi (r_i,r_n)$$

and a similar formula for the derivative of the laplacian. If only the orbital $k$ depends by $a$ we have:

$$\partial_a \vec{\nabla}_i \Phi(r_i,r_j) = \partial_a \vec{\nabla}... ...phi_m(r_j) + \partial_a \phi_k(r_j)\sum_m\lambda_{mk}\vec{\nabla}_i \phi_m(r_i)$$