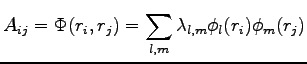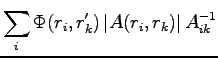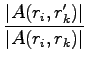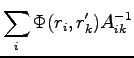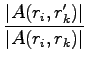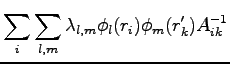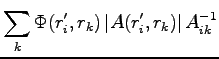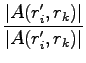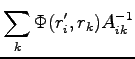Next: Gradients and Laplacian
Up: Local Energy and its
Previous: Derivatives of the Kinetic
Contents
Let us define the matrix 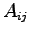 as:
as:
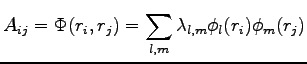 |
(B.8) |
where  are coordinates of spin up electrons and
are coordinates of spin up electrons and  of spin down electrons. For polarized system is possible extend the definition of the geminal wave-function. This generalization was first proposed by Coleman (110). In practise if
of spin down electrons. For polarized system is possible extend the definition of the geminal wave-function. This generalization was first proposed by Coleman (110). In practise if
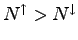 we can define a
we can define a
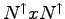 matrix
matrix 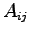 in the following way:
in the following way:
When we move an electron to ratio between the old and the new determinant will be given for a spin down electron:
and for spin up:
For updating the inverse matrix 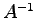 , used here, after a move we follow the simple formula used for the Slater determinant(38) with indices that depend from the spin of the electron.
, used here, after a move we follow the simple formula used for the Slater determinant(38) with indices that depend from the spin of the electron.
Subsections




Next: Gradients and Laplacian
Up: Local Energy and its
Previous: Derivatives of the Kinetic
Contents
Claudio Attaccalite
2005-11-07