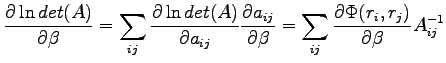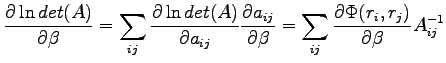Next: Second derivatives
Up: Pairing determinant
Previous: Gradients and Laplacian
Contents
In pairing trial-function the variation of a parameter involves all terms of the matrix and so using D.3 the logarithmic derivatives will be:
If only the k-th orbital depends by  we obtain:
we obtain:
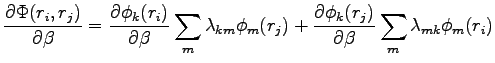 |
(B.15) |
If  is one of the
is one of the  parameter the derivative will be:
parameter the derivative will be:
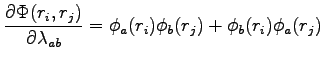 |
(B.16) |
because  matrix is symmetric.
matrix is symmetric.
Claudio Attaccalite
2005-11-07