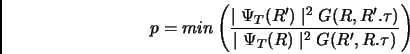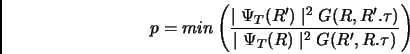Un algoritmo DMC migliorato

Come abbiamo visto, nell'algoritmo DMC noi utilizziamo un'approssimazione che introduce un errore sistematico, dovuto al time-step finito (eq. 2.8); questo errore tende a zero nel limite di piccoli time-step. E' possibile ridurlo utilizzando un algoritmo generalizzato di Metropolis per accettare o rifiutare le mosse proposte dall'equazione di diffusione più il termine di drift. 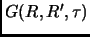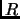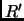Chiamiamo $G(R,R',\tau)$ la probabilità che un walker faccia una mossa, da $R$ ad $R'$ in un tempo $\tau$, secondo l'equazione 2.10. Adesso aggiungiamo la condizione che la mossa sia accettata solo con probabilità:

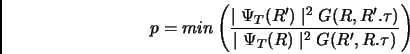$$p=min\left(\frac{\mid \Psi_T(R') \mid^2 G(R,R'.\tau)}{\mid \Psi_T(R) \mid^2 G(R',R.\tau)} \right)$$ (2.14)

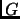La probabilità è scelta in modo da soddisfare il principio del bilancio dettagliato (vedi ref. [33]), in modo che, se $\Psi_T$ coincide con la funzione dello stato fondamentale esatto, il DMC si riduca ad un algoritmo VMC, con le mosse generate dalla funzione $G$. L'inclusione di questo termine di accettazione o rifiuto delle mosse riduce significativamente l'errore dovuto al time-step come è stato verificato in molti lavori (vedi [34]).