




Next: L'effetto del backflow
Up: Fit dei dati Monte
Previous: Fit dei dati Monte
Indice
Indice analitico
Effetti dovuti alle dimensioni finite del sistema
L'uso di una cella di simulazione (N particelle in un volume V) introduce effetti dovuti alle dimensioni finite delle cella. Sebbene noi utilizziamo condizioni periodiche al contorno, che rimuovono gli effetti di superficie caratteristici di una cella isolata, esiste una residua dipendenza dell'energia dalle dimensioni del campione, maggiore per sistemi con interazioni a lungo raggio, perchè la dimensione finita della cella rappresenta un cutoff sulle lunghezze d'onda e perché gli elettroni delle diverse celle ripetute periodicamente nello spazio non sono fra loro indipendenti. Per stimare la nostra energia nel limite termodinamico (sistema infinito e densità costante), vogliamo cercare una forma per questa dipendenza e scrivere la nostra energia come:
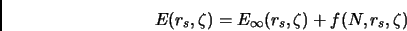 |
(5.1) |
dove
 |
(5.2) |
Possiamo dividere questi effetti in due termini: il primo dovuto ad un sistema di particelle non interagenti, ad il secondo dovuto all'interazione coulombiana.
Il primo termine
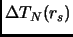 sarà una funzione oscillante di
sarà una funzione oscillante di  . Infatti il vincolo di densità costante (
. Infatti il vincolo di densità costante ( ) implica una variazione delle dimensioni della cella di simulazione (3.1) al variare del numero di particelle. Questo si riflette in una variazione dei vettori
) implica una variazione delle dimensioni della cella di simulazione (3.1) al variare del numero di particelle. Questo si riflette in una variazione dei vettori
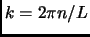 fissati dalle condizioni periodiche al bordo. Il termine
fissati dalle condizioni periodiche al bordo. Il termine
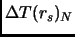 sarà allora proporzionale alla differenza di energia fra un gas ideale a numero di particelle infinito ed uno a numero di particelle N; questa differenza tende a zero come
sarà allora proporzionale alla differenza di energia fra un gas ideale a numero di particelle infinito ed uno a numero di particelle N; questa differenza tende a zero come 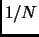 .
.
Il secondo termine
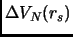 dovuto al potenziale d'interazione invece, in approssimazione Hartree-Fock, decade come
dovuto al potenziale d'interazione invece, in approssimazione Hartree-Fock, decade come 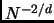 , e puo essere rappresentato da:
, e puo essere rappresentato da:
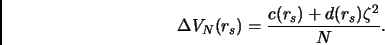 |
(5.3) |
Possiamo allora riscrivere la nostra energia nella forma:
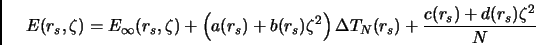 |
(5.4) |
Dopo alcune prove si è deciso di fissare la dipendenza dell'energia cinetica
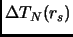 dalla dimensione della cella con fit su sistemi di diverse dimensioni ad
dalla dimensione della cella con fit su sistemi di diverse dimensioni ad 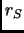 fissato. I parametri così ottenuti, ad ogni singolo
fissato. I parametri così ottenuti, ad ogni singolo 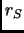 , sono stati, quindi, tenuti fissi, in modo che il fit dei rimanenti parametri nel nostro modello per l'energia non cercasse di compensare qualche piccola discrepanza fra la forma funzionale da noi scelta ed i dati, modificando artificialmente l'estrapolazione di size della parte cinetica. Ciò avrebbe portato, come abbiamo verificato, ad uno sparpagliamento maggiore dei punti rispetto alla curva continua dell'energia.
Il valore del
, sono stati, quindi, tenuti fissi, in modo che il fit dei rimanenti parametri nel nostro modello per l'energia non cercasse di compensare qualche piccola discrepanza fra la forma funzionale da noi scelta ed i dati, modificando artificialmente l'estrapolazione di size della parte cinetica. Ciò avrebbe portato, come abbiamo verificato, ad uno sparpagliamento maggiore dei punti rispetto alla curva continua dell'energia.
Il valore del  ottenuto giustifica pienamente il nostro modello per l'energia.
ottenuto giustifica pienamente il nostro modello per l'energia.
Contemporaneamente a questa tesi sono state proposte da Ceperley, sempre per ovviare al problema delle dimensioni finite, delle condizioni al contorno in cui la funzione d'onda assume una fase diversa da zero passando da una parte all'altra della cella di simulazione; mediando poi su un gran numero di fasi (circa 1000) si ottiene una dipendenza da  dell'energia non oscillante (Twist boundary condition vedi Ceperley [47]). Questa strategia rappresenta probabilmente una buona alternativa da sperimentare in futuro.
dell'energia non oscillante (Twist boundary condition vedi Ceperley [47]). Questa strategia rappresenta probabilmente una buona alternativa da sperimentare in futuro.





Next: L'effetto del backflow
Up: Fit dei dati Monte
Previous: Fit dei dati Monte
Indice
Indice analitico
2001-09-28