Energia di correlazione: dipendenza da $\zeta$ e limiti noti

Possiamo confrontare il nostro modello con il limite noto ad alta densità. Per $r_s \to 0$ abbiamo riportato la nostra dipendenza da $\zeta$ dell'energia di correlazione, insieme a quella esatta ([16]), trovando un buon accordo, come è possibile vedere nella figura 6.1. Altre dipendenze da $\zeta$ utilizzate in precedenti lavori (exchange-like) Ref.[14,15], si rivelano inadeguate non solo per bassi $r_s$ (figura 6.1), ma ancor di più per alti $r_s$. 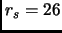In figura 6.2 abbiamo riportato la dipensenza da $\zeta$ dell'energia totale a $r_s =26$ dove, in accordo con i nostri risulati, avviene la transizione di fase al gas completamente polarizzato. A questa densità l'interpolazione exchange-like (qui realizzata utilizzando le nostre energie a $\zeta =0$ e $\zeta =1$) devia significativamente dal risultato QMC. Infatti possiamo vedere che l'exchange-like predice la suddetta transizione da $\zeta =0$ a $\zeta =1$, ma con una barriera di energia fra le due fasi cinque volte più grande del nostro risultato.

Figura: Dipendenza da $\zeta$ dell'energia di correlazione nel limite di alta densità [ $\epsilon_c (r_s\to 0,\zeta)=a_0(\zeta)+O(r_s\ln r_s)$]. Il nostro risultato è confrontato con il valore esatto preso da Ref.[16] e con la dipendenza da $\zeta$ di tipo exchange-like Refs.[14,15].

Figura: Dipendenza da $\zeta$ dell'energia di correlazione alla transizione di fase il nostro risultato è confrontato con la dipendenza exchange-like Ref.[14,15]

.