




Next: Energia nel limite
Up: Teoria perturbativa
Previous: Energia di correlazione
Indice
Indice analitico
Chiamiamo l'ultimo termine dell'equazione (1.11)
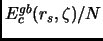 . Vogliamo ora stabilire una relazione fra
. Vogliamo ora stabilire una relazione fra
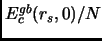 e
e
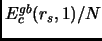 , in modo da poterla utilizzare in seguito come condizione nel limite ad alta densità nel nostro fit. Noi abbiamo per
, in modo da poterla utilizzare in seguito come condizione nel limite ad alta densità nel nostro fit. Noi abbiamo per  e per
e per 
Dove nel caso del gas non polarizzato:
Ponendo in
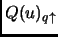 (Eq. 1.10) :
(Eq. 1.10) :
si ottiene
Utilizzando questa relazione è possibile riscrivere
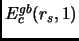 come:
come:
Quindi adesso possiamo scrivere una relazione esplicita fra le due energie:
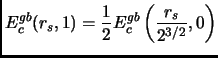 |
|
|
(1.15) |
Questa relazione è importante perché verrà utilizzata come condizione esatta che l'energia di correlazione deve rispettare nel limite di  .
.





Next: Energia nel limite
Up: Teoria perturbativa
Previous: Energia di correlazione
Indice
Indice analitico
2001-09-28
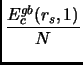
![$\displaystyle \frac{1}{4 \pi ^2 \alpha^2 r_s^2} \int_{-\infty}^{+\infty} du \in...
...\pi q}Q_{q \uparrow} \right) -\frac{\alpha r_s}{2 \pi q} Q_{q\uparrow } \right]$](img97.png)
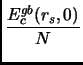
![$\displaystyle \frac{1}{4 \pi ^2 \alpha^2 r_s^2} \int_{-\infty}^{+\infty} du \in...
...+ \frac{\alpha r_s}{\pi q}Q_{q} \right) -\frac{\alpha r_s}{\pi q} Q_{q} \right]$](img99.png)
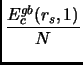
![$\displaystyle \frac{4}{4 \pi ^2 \alpha^2 r_s^2} \int_{-\infty}^{+\infty} du \in...
...}{2 \pi 2^{1/2}q}Q_{q} \right) -\frac{\alpha r_s}{2 \pi 2^{1/2}q} Q_{q} \right]$](img107.png)