




Next: Energia di correlazione a
Up: Teoria perturbativa
Previous: Teoria perturbativa
Indice
Indice analitico
E' possibile espandere l'espressione 1.11 per  nel limite di piccoli
nel limite di piccoli  [8,22]; si ottiene la seguente espressione:
[8,22]; si ottiene la seguente espressione:
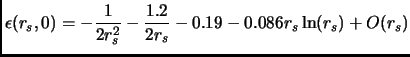 |
|
|
(1.12) |
Molto recentemente l'energia Ŕ stata valutata numericamente all'ordine zero in funzione della polarizzazione [16] ed il risultato Ŕ stato interpolato con la formula (figura 1.1):
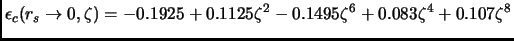 |
|
|
(1.13) |
Figura:
Dipendenza della energia di correlazione dalla polarizzazione di spin nel limite alta densitÓ [
 ] Ref. [16].
] Ref. [16].
![\includegraphics[width=\columnwidth]{figHDa0.eps}](img91.png) |
2001-09-28
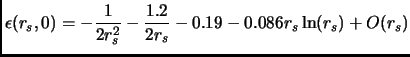
![\includegraphics[width=\columnwidth]{figHDa0.eps}](img91.png)