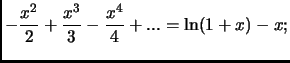Next: Energia di correlazione
Up: Il gas di elettroni
Previous: Energia di correlazione
Indice
Indice analitico
A bassi  è possibile cercare una soluzione al problema in teoria delle perturbazioni , sviluppando l'energia rispetto al termine d'interazione elettrone-elettrone. Questa soluzione si rivela esatta nel limite di
è possibile cercare una soluzione al problema in teoria delle perturbazioni , sviluppando l'energia rispetto al termine d'interazione elettrone-elettrone. Questa soluzione si rivela esatta nel limite di  che va a zero, perché la parte cinetica va come
che va a zero, perché la parte cinetica va come
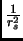 , mentre il potenziale va come
, mentre il potenziale va come 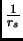 , quindi il sistema si riduce a quello ideale più una correzione piccola che può essere ben rappresentata in teoria delle perturbazioni.
, quindi il sistema si riduce a quello ideale più una correzione piccola che può essere ben rappresentata in teoria delle perturbazioni.
Il primo termine dello sviluppo non è altro che Hartree-Fock. Vogliamo ora scrivere i termini successivi e far vedere come sia possibile risommarli, in parte, seguendo l'approccio di Gell-Mann e Brueckner [19].
Il secondo termine perturbativo è:
Dove  è in unità
è in unità 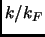 e
e 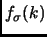 non è altro che la funzione di Fermi a
non è altro che la funzione di Fermi a 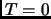 K, cioè la funzione a gradino:
K, cioè la funzione a gradino:
L'energia di second'ordine 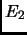 è indipendente da
è indipendente da  ; il primo termine della eq. 1.8 lo chiameremo termine diretto ed il secondo termine di scambio, poiché agisce solo tra elettroni con lo stesso spin. Quest'ultimo è inoltre indipendente da
; il primo termine della eq. 1.8 lo chiameremo termine diretto ed il secondo termine di scambio, poiché agisce solo tra elettroni con lo stesso spin. Quest'ultimo è inoltre indipendente da  poiché in esso appare una
poiché in esso appare una
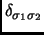 .
.
Il termine di scambio è stato calcolato analiticamente e vale 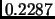 Ry [20].
Ry [20].
Seguendo la procedura di Gell-Mann e Brueckner riscriviamo il termine diretto nella forma:
dove
![$\displaystyle Q_{q \sigma}(u) = \int d^2k \int_{-\infty}^{+\infty} dt e^{-\vert...
...rt(q^2/2 + \vec{q}\cdot \vec{k})} e^{ituq} f_\sigma (k) [ 1 - f_{\sigma} (k+q)]$](img82.png) |
|
|
(1.10) |
prendiamo ora l'ennesimo temine di questo tipo che comparirà nella serie perturbativa; esso ha la forma:
Scrivendoli tutti insieme si ottiene una serie del tipo
sommando tutta la serie, per il solo termine diretto, otteniamo allora per l'energia la seguente espressione:
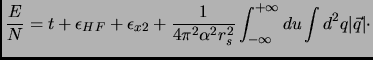 |
|
|
(1.11) |
![$\displaystyle \left [ ln \left( 1+ \frac{\alpha r_s}{2 \pi q} [Q_{q \uparrow}+Q...
...] \right) -\frac{\alpha r_s}{2 \pi q} [Q_{q \uparrow}+Q_{q \downarrow}] \right]$](img86.png) |
|
|
|
L'energia così ottenuta, a meno del termine 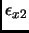 , è la stessa che si otterebbe utilizzando la teoria RPA, sviluppata da Bohm e Pines (vedi [21]).
, è la stessa che si otterebbe utilizzando la teoria RPA, sviluppata da Bohm e Pines (vedi [21]).
Subsections





Next: Energia di correlazione
Up: Il gas di elettroni
Previous: Energia di correlazione
Indice
Indice analitico
2001-09-28
![$\displaystyle \frac{E_2}{N} = - \frac{1}{8 \pi ^3}\sum_{\sigma_1 \sigma_2} \int...
...1 \int d^2k_2 f_{\sigma_1}f{\sigma_2}[1-f_{\sigma_1}(\vec{k_1}+\vec{q}) ] \cdot$](img70.png)
![$\displaystyle \left[1 - f_{\sigma_2} (\vec{k_{2}}+\vec{q})\right]\left(\frac{1}...
...{k_1}+\vec{k_2}\vert}\right)\frac{1}{q^2 + \vec{q}\cdot(\vec{k_1}+\vec{k_2})} =$](img71.png)
![$\displaystyle \frac{E_2^{dir}}{N} = - \frac{1}{4 \pi ^2 \alpha^2 r_s^2}\frac{(-...
... \left ( \frac{\alpha r_s}{2 \pi q} [Q_{q \uparrow}+Q_{q \downarrow}] \right)^2$](img81.png)
![$\displaystyle \frac{E_n^{dir}}{N} = - \frac{1}{4 \pi ^2 \alpha^2 r_s^2}\frac{(-...
...left ( \frac{\alpha r_s}{2 \pi q} [Q_{q \uparrow}+Q_{q \downarrow}] \right)^n .$](img83.png)