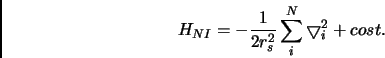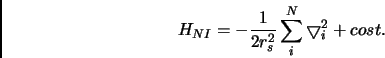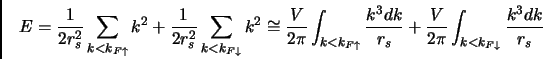Next: Hartree-Fock Up: Il gas di elettroni Previous: Definizioni utili Indice Indice analitico

Gas di elettroni indipendenti

La prima approssimazione possibile, per risolvere il nostro problema, consiste nel trascurare l'interazione fra gli elettroni, quindi la nostra Hamiltoniana sarà:

$\begin{displaymath} H_{NI} = - \frac{1}{2r_s^2} \sum _i ^N \bigtriangledown _i^2 + cost. \end{displaymath}$

Sappiamo che un determinante di Slater di onde piane è una soluzione di questa Hamiltoniana; vogliamo trovare l'energia in funzione della polarizzazione. Il vettore di Fermi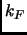

è definito da

$\begin{displaymath} \frac{N}{V} = n = \frac{k_F^2}{4 \pi} \end{displaymath}$

Dove

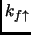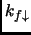
è l'area del nostro sistema. Analogamente possiamo definire $k_{f\uparrow}$ e $k_{f\downarrow}$

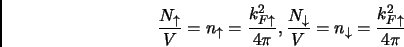$\begin{displaymath} \frac{N_\uparrow}{V} = n_{\uparrow}=\frac{k_{F\uparrow}^2}{4... ..._\downarrow}{V} = n_{\downarrow}=\frac{k_{F\uparrow}^2}{4 \pi} \end{displaymath}$

(1.5)

Ora prendiamo come funzione d'onda un determinante di onde piane, e lo sostituiamo nell'eq. di Schrodinger ed otteniamo che l'energia totale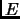

è data da:

$\begin{displaymath} E = \frac{1}{2r_s^2} \sum _{k<k_{F\uparrow}}{k^2}+ \frac{1}{... ... + \frac{V}{2 \pi } \int_{k<k_{F\downarrow}} \frac{k^3dk}{r_s} \end{displaymath}$

integrando ed utilizzando le relazioni 1.5, 1.4 abbiamo allora:

$\begin{displaymath} \frac{E}{N} = \frac{1}{2r_s^2}( 1 + \zeta ^2) \end{displaymath}$

(1.6)

2001-09-28